Teorema di Pitagora: dall'enunciato alla dimostrazione facile
In questo articolo troverai l’enunciato e le formule del famoso
Teorema di Pitagora. E’ importante che tu conosca e sappia usare bene il Teorema di Pitagora in quanto è fondamentale per lo studio della geometria, della geometria sul piano cartesiano e della
trigonometria. Nonostante sia un argomento molto studiato a scuola, è possibile che tu non abbia ben capito come si applica, quale sia la formula e come risolvere esercizi e problemi in cui devi applicare il Teorema di Pitagora. Pronto per scoprire tutto sul Teorema di Pitagora? La matematica non sarà più un problema: vediamo insieme
formule, enunciati e dimostrazioni del Teorema di Pitagora!
Teorema di Pitagora: cosa imparerai oggi
Dopo la lettura dei paragrafi seguenti sarai in grado di dire quando si può applicare il Teorema di Pitagora e di usare le formule che derivano da questo importante teorema.
Cosa devi sapere:
Suggerimento:
- procurati dei fogli a quadretti e durante la lettura prova a riprodurre i disegni geometrici che trovi di seguito e scrivi anche le formule presenti.
Teorema di Pitagora: cos'è e perché si chiama così
Il Teorema è stato studiato secoli e secoli prima della nascita del filosofo Pitagora! Il primo enunciato del Teorema è stato trovato su una tavoletta babilonese risalente addirittura al 1900-1600 avanti Cristo. Pitagora, che è vissuto tra il 560-480 avanti Cristo, è stato però il primo ad aver dato dimostrato il teorema, che ha preso quindi il suo nome.
Il Teorema di Pitagora si applica
solo ai
triangoli rettangoli, ossia a quei triangoli
dove uno degli angoli è un angolo retto (misura cioè 90°).
Dimostrazione facile del Teorema di Pitagora
Consideriamo il triangolo rettangolo ABC, dove l’angolo è un angolo retto.
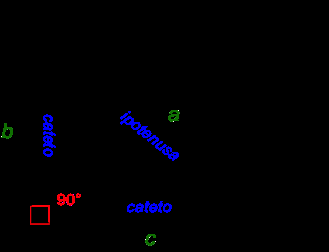
In un qualsiasi triangolo rettangolo il lato di fronte l’angolo retto viene detto
ipotenusa, ed è il lato più lungo del triangolo, mentre gli altri due lati sono detti
cateti. Nel caso del nostro triangolo ABC il lato BC è l’
ipotenusa e i lati AC e AB e sono i
cateti.
Teorema di Pitagora: definizione e formula
Il Teorema di Pitagora dice che (enunciato 1):
la somma delle lunghezze al quadrato dei cateti è uguale al quadrato della lunghezza dell’ipotenusa
Applicando il teorema di Pitagora al nostro triangolo abbiamo che:
Se supponiamo che nel nostro triangolo l’ipotenusa BC abbia una lunghezza pari ad
a, il cateto AC uguale a
b ed il cateto AB uguale a
c, cioè
abbiamo che la formula del Teorema di Pitagora diventa (sostituendo i valori delle lunghezze dei lati del triangolo):
Conseguenze del Teorema di Pitagora
La formula del Teorema di Pitagora ci permette di calcolare la lunghezza di un lato di un triangolo rettangolo noti gli altri due.
Facciamo degli esempi.
Esempio 1 - Supponiamo che per il nostro triangolo siano note le lunghezze dei cateti e vogliamo calcolare la lunghezza dell’ipotenusa che non è nota, ossia:
Applicando la formula del Teorema di Pitagora abbiamo che:
Osserviamo che la formula del Teorema di Pitagora ci permette di calcolare
il quadrato dell’ipotenusa. Per ottenere la
lunghezza dell’ipotenusa è necessario calcolare la radice quadrata, ossia:
Note le lunghezze dei due cateti, applicando il Teorema di Pitagora abbiamo calcolato la lunghezza dell’ipotenusa.
Esempio 2 - Supponiamo che per il nostro triangolo siano note la lunghezza di un cateto e dell’ipotenusa: vogliamo calcolare la lunghezza dell’altro cateto, ossia:
Applicando la formula del Teorema di Pitagora abbiamo che:
Sottraendo AC da ambo i membri della formula precedente, abbiamo che:
Sostituendo i valori delle lunghezze dei lati del triangolo, otteniamo:
da cui
Nota la lunghezza di un cateto e dell’ipotenusa, applicando il Teorema di Pitagora abbiamo calcolato la lunghezza dell’altro cateto.
Teorema di Pitagora: approfondimento ed enunciato 2
Il Teorema di Pitagora è noto anche con il seguente enunciato (enunciato 2):
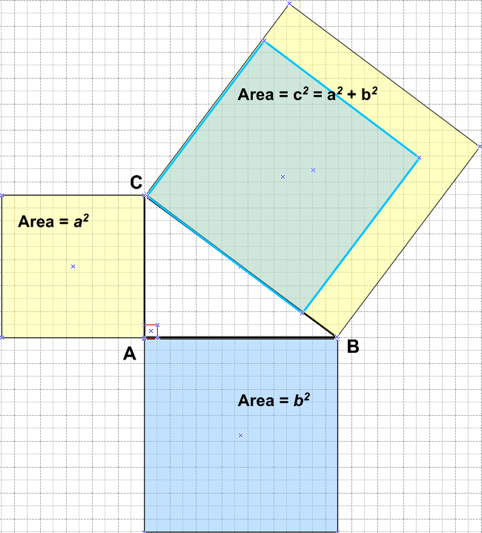
la somma delle aree dei quadrati costruiti sui cateti è uguale all’area del quadrato costruito sull’ipotenusa.
L’enunciato 1 e l’enunciato 2 esprimono lo stesso concetto: l’enunciato 2 però è legato alla dimostrazione del teorema fatta da Pitagora (che qui non affrontiamo).
- Osservazione 1: I vertici di un qualsiasi poligono (compresi i triangoli) sono sempre indicati con le lettere maiuscole.
- Osservazione 2: E’ bene indicare sempre la posizione dell’angolo retto in un triangolo rettangolo.
Teorema di Pitagora: riepilogo
Il Teorema di Pitagora è valido solo per i triangoli rettangoli e la sua formula ci permette di calcolare la lunghezza di un lato di un triangolo rettangolo noti gli altri due.
